
In case you're wondering, the strange object you see above is a four-dimensional hyper-cube, or rather it is a representation of a four-dimensional hyper-cube, or if you prefer, a TESSERACT, having eight cubes as exterior faces. It has thirty two linear edges, and sixteen corners where four edges meet at ninety degree angles to one another!
Impossible you say? Of course it would be impossible to build such a structure in three-dimensional space, but if space were four-dimensional, you could have four orthogonal, or perpendicular vectors passing through a single point, and all four vectors would be at ninety degrees to one another.
This is an introduction to multi-dimensional geometry, and in geometry, you can have as many dimensions as you like. I'm only going to take you up to seven dimensions since it's a real pain in the tukus to calculate the geometric properties of structures having more dimensions.
Of course, you're probably asking, BUT ISN'T TIME THE FOURTH DIMENSION? And you're right, according to Einstein's General Theory Of Relativity, time would be the fourth dimension, and time is measured in seconds, minutes, hours, days, weeks, months, years, etc. etc. so in Relativity Theory, the fourth dimension is not measured in inches and feet, etc.
Also, in the realm or Quantum Physics, ELEVEN DIMENSIONS are needed to describe all the known properties of sub-atomic particles, and of course, all the higher dimensions are NOT measured in linear units like inches, feet, years, centimeters, meters, etc. etc. Only the first three dimensions, the dimensions of space in which we move about are measured in linear units, while time is the fourth dimension. The dimensions beyond the fourth dimension are units used in quantum physics, which we won't go into here on this topic.
So . . . for now we are talking about Euclidean Geometry which is normally flat two-dimensional plane geometry and three-dimensional solid geometry. But you can have as many dimensions as you like. And so, for this demonstration, we are going to pretend that these higher dimensions are spacial dimensions measured in inches, feet, yards, etc. etc. or metric units if you prefer, millimeters, centimeters, meters, etc. etc. OK?
And so, let us proceed on our outward journey to higher dimensions. We will start out real simple like, and then gradually move on top more complex dimensions.
So, hang on to your hats! This is going to be quite a wild ride!!!
 To make things simple, I will take you step by step up through the dimensions, so let us start at the beginning. As we all know, the space we move about in, is three-dimensional. When you stand in the center of your room, you can step forward or backward, that's one dimension. You can step to the left, or to the right, that's two dimensions. And of course you can jump up and down, that's your third dimension.
To make things simple, I will take you step by step up through the dimensions, so let us start at the beginning. As we all know, the space we move about in, is three-dimensional. When you stand in the center of your room, you can step forward or backward, that's one dimension. You can step to the left, or to the right, that's two dimensions. And of course you can jump up and down, that's your third dimension.
But if you could step off in some mysterious direction, that is at a ninety degree angle to all the three dimensions of your room, you would simply move off into this mysterious fourth dimension, and of course, to anybody else in the room, you would have simply disappeared, vanished into thin air, Like, POOF! No one in three-dimensional space will be able to see you, because to them, you will have simply vanished. But you will be able to look back from where you came, and see things as you have never seen them before! You will for the very first time in your life, see things as they really are!
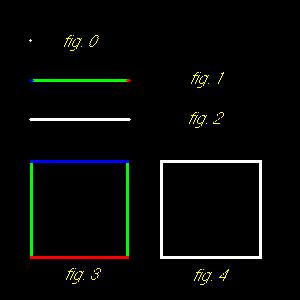
But lets make this simple. so, lets start off with something that's zero dimensional, like a point, a small dot, having no length, width, or height. First of all, let's picture in our minds, an empty black void, and all you can see is one tiny luminous point (fig.0) which has zero dimensions. Now, imagine this point moving through this void, leaving a luminous trail as it moves (fig.1) and the further it moves, the longer the trail becomes. This would be just a straight line, having only one dimension.
In the picture (fig.1) the blue dot represents the point in it's original position, while the red dot represents the point in it's new position where it came to a stop, and the green line represents the distance that it moved. The result is a line segment (fig.2) having two exterior end points and of course one interior line segment. We have now entered the first dimension, that being of a single line.
Now let's open the gate to the second dimension. We shall move the entire line segment, in a direction that is perpendicular, or at a ninty degree angle to itself, and let's move the line segment the same amount of distance (fig.3) in the second dimension, as we had moved the zero dimensional point.
Again the blue line represents the line in the original position, the red line represents where it stopped in it's new position, and the two green lines represents the motion of the two end points. The result is a square (fig.4) having four corners where two linear edges meet at ninety degree angles to one another. The square has four exterior linear edges, and what was once the interior segment of a single one-dimensional line, is now the exterior edge of the two-dimensional square, and of course the square has one interior area.
Let us say we had moved the point, about 10 units, and the line 10 units. The units could be measured in inches, feet, centimeters, or meters. But in our example, we will say we had moved the point and the line, ten feet. We would have a square that is 10 x 10 feet with an interior area that is 100 square feet, and a perimeter (total distance around all four sides) of 40 feet. So, the square has only two dimensions, length and width, but no height, or thickness.
If we were to live in a world of only two dimensions, you would only be able to view the square from the edge, and you could not see the interior area. Life in a two-dimensional world would be rather plane indeed! Everything about people would be flat, including their heads, wallets, and beer!
Now let us open the gate to the third dimension, out here where we live, and look down upon the humble square, and see it as it truly is! Because we dwell in the world of three dimensions, we can see all four exterior edges, and the interior area.
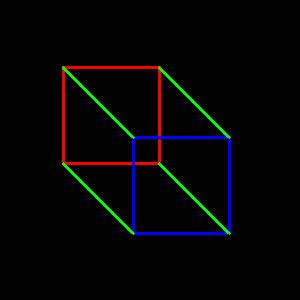 This time we start with the square in it's original position, as represented by the blue square, and we shall move it ten feet until it stops at it's new position, as represented by the red square. Notice that as the four points on the corners moved, they traced out four more linear edges, as represented by the green lines.
This time we start with the square in it's original position, as represented by the blue square, and we shall move it ten feet until it stops at it's new position, as represented by the red square. Notice that as the four points on the corners moved, they traced out four more linear edges, as represented by the green lines.
The result is a cube, having four corners in the original position, and four corners in the new position, for a total of eight corners, and at each corner, three linear edges meet, and they are at ninety degree angles to one another. Also notice, that at each linear edge, two exterior surfaces meet one another at ninety degree angles.
There are four sides on the square in the original position, and four sides on the square in the new position, and as the four points on the corners moved, they traced out four more lines, or linear edges, giving the cube a total of twelve linear edges. Then of course, with the square in it's original position, and the square in it's new position, and the four linear edges moving, they would sweep out four more square areas, giving a total of six exterior faces on the cube. So, what was once the interior area of the two-dimensional square, is now an exterior surface of the cube. The end result once again, as represented by the white cube, is a three-dimensional polyhedron, an hexahedron, commonly known as the cube. Now we have our majestic cube, with eight corners, twelve linear edges, and six external square surfaces, and of course, it has one interior region, that we refer to as the volume of the cube.
 Because the cube measures ten feet wide, ten feet long, and ten feet tall, it has an interior volume of 10x10x10=1000 cubic feet. The six squares are 10x10=100 square feet each, so the cube a total surface area of 100x6=600 square feet. Also, the twelve linear edges being ten feet each, has a total length of 10x12=120 linear feet.
Because the cube measures ten feet wide, ten feet long, and ten feet tall, it has an interior volume of 10x10x10=1000 cubic feet. The six squares are 10x10=100 square feet each, so the cube a total surface area of 100x6=600 square feet. Also, the twelve linear edges being ten feet each, has a total length of 10x12=120 linear feet.
Since the cube is represented by a wire frame type of diagram, we can see it has six square surfaces, and twelve linear edges, but if we were to look at a solid cube we could only see a maximum of three faces, and we would not be able to see the interior. That is because we live and move about in only three dimensions of space. But if we could open the gate to the fourth dimension, and step through, we could then see the cube as it really is. The truth is, that we NEVER actually see the world around us as it really is! We can look at two-dimensional figures, polygons, like triangles, squares, pentagons, hexagons, heptagons, octagons, etc. etc. and see how many sides they have, and their interior areas. But when we look at three-dimensional objects, we can only see what is presented to us at any given moment in time. For example: when you're sitting in your living room, watching your TV set, which is cubical in shape, if you're sitting directly in front, you only see the screen on the front face. Then if you stand up, you can see the front screen, and the top surface. Then if you step to one side, you can see the front screen, top surface, and one of the sides. But you can't see the other side, the bottom, or the back. Also you can't see what's inside. The other three surfaces and the interior are hidden from view.
But if you could move off into the fourth dimension, you would be able to have a direct perpendicular view of all six exterior surfaces, and the interior! You would be able to work on the electronics inside your TV set, without having to remove the back panel! You could remove the contents of any sealed container, without ever breaching the exterior surface of said container! A four-dimensional doctor could perform internal surgery on a three-dimensional patient without ever having to cut through the skin surface. A four-dimensional bank robber could remove the money from a three-dimensional vault, without ever having to open it first! If you were four-dimensional, you could unhook the links of a three-dimensional chain, without having to cut any of the links! That is because, everything that appears to be closed off in three dimensions would be open to the fourth dimension!
Now then, boys and girls! Let us proceed to open the gates to the fourth dimension, and I shall introduce you to our weird little friend, THE FOUR-DIMENSIONAL HYPER-CUBE! Naturally, since we live in a world of only three physical dimensions, we can not actually build a hyper-cube. But we can represent one on a two-dimensional plane, just as we can draw three-dimensional objects on a sheet of paper. Artists do it all the time, so we shall do the same, using wire frame diagrams. Are you ready to join The Fat Man, as he take you on a journey through The Fourth Dimension, and beyond! Don't be scared now!
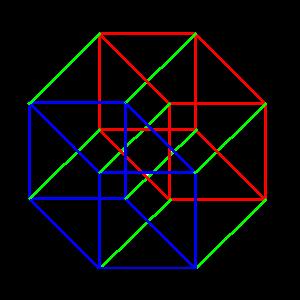 OK! Here we go, off on our little journey into four-dimensional hyper-space! We shall start with our cube in it's original position, as represented by the blue cube. Now we shall move our once majestic, but now humbled cube, out of our three-dimensional realm, and POOF! It has disappeared from the view of all onlookers who have stayed behind! But since we are following it, we see it moving through hyper-space for a distance of ten feet, to come to rest in it's new position, as represented by the red cube.
OK! Here we go, off on our little journey into four-dimensional hyper-space! We shall start with our cube in it's original position, as represented by the blue cube. Now we shall move our once majestic, but now humbled cube, out of our three-dimensional realm, and POOF! It has disappeared from the view of all onlookers who have stayed behind! But since we are following it, we see it moving through hyper-space for a distance of ten feet, to come to rest in it's new position, as represented by the red cube.
Now the cube in it's original position has eight corners, and the cube in the new position has eight corners, giving the hyper-cube a total of sixteen corners. Also notice, the cube in the original position has twelve linear edges, and the cube in the new position has twelve linear edges, and as the cube moved, the eight points on the corners moved, as represented by the green lines, giving us a total of thirty two linear edges.
At each of the sixteen corners, four linear edges meet at ninety degrees to one another, and at each linear edge, three square surfaces also meet at ninety degree angles to one another. A physical impossibility in three-dimensional space, but not impossible in four-dimensional hyper-space! The cube in the original position has six square faces, and the cube in the new position has six square faces, and as the twelve linear edges moved, they swept out twelve more square areas, thus giving us a total of twenty four square faces.
Finally, we have one cube in the original position, one cube in the new position, and as the six square faces moved, they swept out six more cubical regions in hyper-space, giving a total of eight exterior cubical hyper-surfaces. So, what was once the interior volume of the cube, is now the exterior hyper-surface of the hyper-cube! Neat! Eh? What do you think of our little journey so far?
 So, once again, ladies and gentlemen, boys and girls, behold THE MAJESTIC HYPER-CUBE! This little beastie has thirty two linear edges, measuring ten feet each, having a total of 10x32=320 linear feet. It has twenty four square faces, each measuring 10X10=100 square feet for a total of 100x24=2400 square feet, also eight cubic hyper-surfaces, each measuring 10x10x10=100 cubic feet, with a total hyper-surface volume of 100x8=800 cubic feet, and an interior hyper-vulume of 10x10x10x10=10000 hyper-cubic feet!
So, once again, ladies and gentlemen, boys and girls, behold THE MAJESTIC HYPER-CUBE! This little beastie has thirty two linear edges, measuring ten feet each, having a total of 10x32=320 linear feet. It has twenty four square faces, each measuring 10X10=100 square feet for a total of 100x24=2400 square feet, also eight cubic hyper-surfaces, each measuring 10x10x10=100 cubic feet, with a total hyper-surface volume of 100x8=800 cubic feet, and an interior hyper-vulume of 10x10x10x10=10000 hyper-cubic feet!
Since this is a wire frame diagram, we can see that it has sixteen corners, thirty two edges, twenty four square faces, and eight external cubical hyper-surfaces! But if this were actually a four-dimensional, hyper-solid polytope, and if we were four-dimensional beings, we would not be able to see all of the features of the hyper-cube. We would only be able to see a maximum of four of its cubical hyper-surfaces. The other four would be hidden, and we would not be able to see the interior of the hyper-cube. To be able to see the hyper-cube as it really is, we would have to open the gates to the fifth dimension, and step through! That's right boys and girls! This is not the end! I told you we are taking this up to seven dimensions! Not only that, but after we're done exploring cubical structures in higher dimensions, were going to do a detailed study of rectangular structures, all the way up to the seventh dimension! So, hang on to your hats, because it's going to be one really wild ride!
So now it's Onward! On to The Fifth Dimension, and I'm not talking about a 1960's rock group either! How do you like our little journey so far? Not the kind of geometry they taught us in high school, or our parents, and even grand parents for that matter!
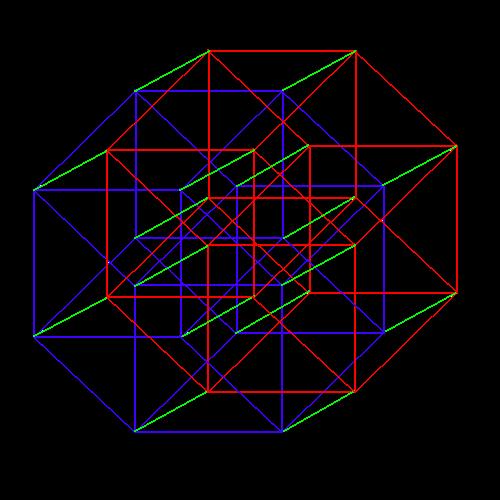 OK, boys and girls! Here we go again! As usual, we start out with our four-dimensional hyper-cube cube in it's original position as represented by the blue lines. We shall now move it out into the fifth dimension, and again, POOF! It disappears from the view of any four-dimensional onlookers! But since we're hanging on for the ride, we have now entered the fifth dimension, and we see our hyper-cube moving another ten feet until is comes to rest in it's new position, as represented by the red lines, and as usual, the green lines indicate it's motion through the higher dimension.
OK, boys and girls! Here we go again! As usual, we start out with our four-dimensional hyper-cube cube in it's original position as represented by the blue lines. We shall now move it out into the fifth dimension, and again, POOF! It disappears from the view of any four-dimensional onlookers! But since we're hanging on for the ride, we have now entered the fifth dimension, and we see our hyper-cube moving another ten feet until is comes to rest in it's new position, as represented by the red lines, and as usual, the green lines indicate it's motion through the higher dimension.
The hyper-cube, which I will now refer to as a "TESSERACT" from now on, has sixteen corners in the original position, and sixteen corners in it's new position, giving the five-dimensional hyper-tesseract a total of thirty two corners, and at each corner, we have five linear edges meeting one another at ninety degree angles!
This is impossible to visualize in your mind, but we won't let that stop us! The tesseract in the original position has thirty two linear edges, and in the new position, thirty two more linear edges, and as the points on the sixteen corners moved, they traced out sixteen more linear edges, as indicated by the green lines, giving a total of eighty linear edges, and at each edge, four square faces meet one another at ninety degree angles. Impossible you say? In three-dimensional space, yes, but since we're now in the fifth dimension, it is mathematically possible. The four-dimensional tesseract in it's original position has twenty four squares, and in it's new position, twenty four more squares, and as the thirty two linear edges moved, they swept out thirty two more square areas, giving us a total of eighty square faces.
The four-dimensional tesseract in its original position has eight cubical hyper-surfaces, and in it's new position, another eight cubical hyper-surfaces, and as the twenty four squares moved, they swept out twenty four more cubical volumes, giving a total of forty cubes.
Finally, we had the four-dimensional tesseract in it's original position, and the tesseract in its new position, and as the eight cubes moved, they swept out eight more hyper-cubic regions, giving us a total of ten external hypercubes!
So, once again, our five-dimensional hyper-tesseract, has thirty two corners where five edges meet at ninety degree angles to one another, eighty linear edges where four squares meet at ninety degree angles, eighty squares, forty cubes, and ten hyper-cubes!
 When you look at these wire-frame diagrams, you can pick out all the properties if you really concentrate, and of course, I used colored diagrams to make the task a lot easier, so you can make out ALL the cubes and squares, if you really concentrate.
When you look at these wire-frame diagrams, you can pick out all the properties if you really concentrate, and of course, I used colored diagrams to make the task a lot easier, so you can make out ALL the cubes and squares, if you really concentrate.
But if this were really a "solid" structure, in five dimensions, and if we were actually five-dimensional beings, we would only be able to see a maximum of five of the hyper-cubes on the four-dimensional "surfaces", while the other five hyper-cubes and the five-dimensional interior would be hidden from view.
The total length of the eighty linear edges is 10x80=800 feet. The total area of the eighty squares is 80x(10x10)=800 square feet. Total volume of the forty cubes is 40x(10x10x10)=40000 cubic feet. The total four-dimensional hyper-hyper-surface volume is 10x(10x10x10x10)=100000 hyper-cubic feet, and the five-dimensional hyper-hyper-volume naturally would be 10x10x10x10x10=100000 hyper-hyper-cubic feet.
Oh my! It just keeps on getting better! Doesn't it? Are you sure you want to go on? If so, then keep on reading, boys and girls! On the other hand, if you are afraid to continue, and you feel that you're about to freak out, then click here to EXIT this page and go back to where you came from.
But for all of you brave souls who are not afraid to venture forth, keep scrolling down to continue reading. I promise you, that you won't be disappointed, and when you're done, I believe you will never see the world around you in the same way you have seen it all your lives. You'll come away with a different point of view, knowing that all that you see around you, are mere shadows of what may exist in higher dimensions, just as the two-dimensional square is a mere shadow of the three-dimensional cube, the cube is only a mere shadow of the four-dimensional hypercube, and the hyper-cube, or TESSERACT, is a mere shadow compared to the five-dimensional HYPER-TESSERACT! And what you have seen so far, is merely a shadow of what awaits us in The Sixth Dimension!
Now then, boys and girls! Are you ready to travel outward through the gates of The Sixth Dimension? Of course you are, else you wouldn't be here! So hang on, as our wild ride continues, onward, ever onward! We shall now move our five-dimensional HYPER-TESSERACT through the realm of the sixth dimension, and again, POOF! It disappears from the view of any five-dimensional onlookers, but since we're still hanging on for the ride, we shall follow it until it has moved another ten feet, to come to rest again, in a new position, parallel to it's original position.
 The five-dimensional HYPER-TESSERACT in it's original position has thirty two corners, and in it's new position, thirty two more corners, giving us a six-dimensional structure with a total of 64 corners, and at each corner, we now have six linear edges meeting one another at ninety degree angles!
The five-dimensional HYPER-TESSERACT in it's original position has thirty two corners, and in it's new position, thirty two more corners, giving us a six-dimensional structure with a total of 64 corners, and at each corner, we now have six linear edges meeting one another at ninety degree angles!
The five-dimensional HYPER-TESSERACT in it's original position has eighty linear edges, and in the new position, it also has eighty linear edges, and when the thirty two points on the corners moved, they traced out thirty two more linear edges, giving us a total of one hundred and ninety two linear edges, and at each of the edges, we have five square faces meeting at ninety degree angles. Don't try to visualize this in your mind, you'll get a headache! But let us continue.
The five-dimensional HYPER-TESSERACT in its original position has eighty square faces, and in the new position, eighty more square faces, and as the eighty liner edges moved, they swept out eighty more square areas, giving us a total of two hundred and forty square faces.
The five-dimensional HYPER-TESSERACT in it's original position has forty cubes, and and in the new position, forty more cubes, and as the eighty square faces moved, they swept out eighty more cubical regions, giving us a total of one hundred and sixty cubes! The five-dimensional HYPER-TESSERACT in it's original position has ten, four-dimensional hyper-cubes, and in its new position, ten more, four-dimensional hyper-cubes, and as the forty cubes moved, they swept out forty more hyper-cubic regions, giving us a total of sixty, four-dimensional hyper-cubes.
Finally, we have one, five-dimensional HYPER-TESSERACT in it's original position, and another five-dimensional HYPER-TESSERACT in its new position, and as the ten, four-dimensional hyper-cubes moved, they swept out ten more five-dimensional regions giving us a total of twelve, five-dimensional, exterior "surfaces", with the interior six-dimensional "volume" of our weird thing-a-ma-jig!
Again, let's us review the properties of the six-dimensional thing-a-ma-jig. It has sixty four corners, where six linear edges meet one another at ninety degree angles. One hundred and ninety two linear edges, where five squares meet at ninety degree angles. Two hundred and forty squares, one hundred and sixty cubes, sixty four-dimensional hyper-cubes or TESSERACTS, and twelve, five-dimensional exterior, HYPER-TESSERACTS. Really simple! Eh? NOT!
 If you study the wire frame diagram closely, you might be able to pick out all the lines, squares, cubes, hyper-cubes, etc. etc. Of course you'll probably strain your eyes, or go crazy in the process. But if this were actually a "solid" structure in six dimensions, and if we were six-dimensional beings, we would only be able to see a maximum of six of the twelve, five-dimensional, exterior HYPER-TESSERACTS. The other six exterior HYPER-TESSERACTS, and the interior six-dimensional "volume" would be hidden from view.
If you study the wire frame diagram closely, you might be able to pick out all the lines, squares, cubes, hyper-cubes, etc. etc. Of course you'll probably strain your eyes, or go crazy in the process. But if this were actually a "solid" structure in six dimensions, and if we were six-dimensional beings, we would only be able to see a maximum of six of the twelve, five-dimensional, exterior HYPER-TESSERACTS. The other six exterior HYPER-TESSERACTS, and the interior six-dimensional "volume" would be hidden from view.
The total length of all one hundred and ninety two linear edges would be 10x192=1920 feet. The total area of all two hundred and forty squares is 240x(10x10)=24000 square feet. The total volume of all one hundred and sixty cubes is 160x(10x10x10)=160000 cubic feet. The total hyper-volume, of all the sixty, four-dimensional hyper-cubes is 60x(10x10x10x10)=600000 hyper-cubic feet. The total five-dimensional surface hyper-hyper "volume" of the twelve exterior HYPER-TESSERACTS would be 12x(10x10x10x10x10)=1200000 hyper-hyper cubic feet, and the interior six-dimensional hyper-hyper-hyper "volume" is 10x10x10x10x10x10=1000000 hyper-hyper-hyper cubic feet.
Too bad mathematicians have not invented new names to gives these multi-dimensional structures beyond the fourth dimension. Perhaps one of these days I'll invent some new names to call these things! Before we continue you may want to go back and review what we have covered so far, and then you'll stay confused! I trust I make myself obscure! Do you still want to go on? OK, then keep hanging on to your hats, because we're now going to enter The Seventh Dimension.

I am NOT about to stay up all night, trying to design a seven-dimensional what-cha-call-it! But we can still describe all the geometric properties. Just remember, that every time a zero-dimensional point moves, it traces a one-dimensional line. Whenever a line moves, it sweeps out a two-dimensional square. when a square moves, it sweeps out a three-dimensional cube. when a cubes moves, it sweeps out a four-dimensional hyper-cube, or TESSERACT. Whenever a TESSERACT moves, it sweeps out a five-dimensional HYPER-TESSERACT, and when a HYPER-TESSERACT moves, it sweeps out a six-dimensional thing-a-ma-jig.
So now were going to open the gates to The Seventh Dimension, and enter therein. We shall now move the six-dimensional thing-a-ma-jig, another ten feet to generate the seven-dimensional what-cha-call-it! OK, boys and girls! Hang on as we move the six-dimensional thing-a-ma-jig out into the seventh dimension, and again, POOF! It disappears from any six-dimensional onlookers, but since we're moving out into the seventh dimension along with it, we can follow it until it comes to rest in it's new position.
We start out with the six-dimensional thing-a-ma-jig in it's original position. It has sixty four corners, and when moved to it's new position, we have sixty four more corners, giving our seven-dimensional what-cha-call-it a total of one hundred and twenty eight corners, and at each corner, seven linear edges meet one another at ninety degree angles!
The six-dimensional thing-a-ma-gig in it's original position has one hundred and ninety two linear edges, and in it's new position, one hundred and ninety two more linear edges, and as the sixty four corners moved, they traced out sixty four more lines, giving us a total of four hundred and fourty eight linear edges.
The six-dimensional thing-a-ma-jig in it's original position has two hundred and fourty squares, and in it's new position, another two hundred and forty squares, and as the one hundred and ninety two edges moved, they swept out one hundred and ninety two more squares, giving us a total of six hundred and seventy two squares.
The six-dimensional thing-a-ma-jig in it's original position has one hundred and sixty cubes, and in its new position another one hundred and sixty cubes, and as the two hundred and forty squares moved, they swept out two hundred and forty more cubes, giving us a total of five hundred and sixty cubes!
The six-dimensional thing-a-ma-jig in it's original position has sixty, four-dimensional hyper cubes, and in its new position, another sixty hyper-cubes, and as the one hundred and sixty cubes moved, they swept out one hundred and sixty more four-dimensional hyper-cubes, giving us a total of two hundred and eighty hyper-cubes, or tesseracts!
The six-dimensional thing-a-ma-jig in it's original position has twelve, five-dimensional hyper-tesseracts, and in it's new position, another twelve hyper-tesseracts, and as the sixty hyper-cubes moved, they swept out sixty more five-dimensional hyper-tesseracts, giving us a total of eighty four, five-dimensional hyper-tesseracts!
Finally, we have the six-dimensional thing-a-ma-jig in it's original position, and in its new position, and as the twelve, five-dimensional hyper-tesseracts moved, they swept out twelve more, six-dimensional thing-a-ma-jiggies, giving us a total of fourteen external six-dimensional thing-a-ma-jiggies!
Once again, the properties of the seven-dimensional what-cha-call-it is that it has one hundred and twenty eight corners, four hundred and forty eight linear edges, six hundred and seventy two squares, five hundred and sixty cubes, two hundred and eighty hyper-cubes, or tesseracts, eighty four, five-dimensional hyper-tesseracts, and fourteen exterior six-dimensional thing-a-mag-jiggies!
If the seven-dimensional what-cha-call-it were a "solid" structure, and if we were seven-dimensional beings, we would only be able to see a maximum of seven of the fourteen external, six-dimensional thing-a-ma-jiggies.
The total length of the four hundred and forty eight linear edges is 10x448=4880 feet. The total area of the six hundred and seventy two squares is 672x(10x10)=6720 square feet. The total volume of the five hundred and sixty cubes is 560x(10x10x10)=560000 cubic feet. The total four-dimensional hyper-volume of the two hundred and eighty hyper-cubes is 280x(10x10x10x10)=2800000 hyper-cubic feet. The total five-dimensional hyper-hyper volume of the eighty four, five-dimensional hyper-tesseracts is 84x(10x10x10x10x10=8400000 hyper-hyper cubic feet. The exterior "surface" hyper-hyper-hyper-volume of the fourteen, external, six-dimensional thing-a-ma-jiggies is 14x(10x10x10x10x10x10)=14000000 hyper-hyper-hyper-cubic feet, and the internal seven-dimensional hyper-hyper-hyper-hyper volume is 10x10x10x10x10x10x10=10000000 hyper-hyper-hyper-hyper-cubic feet!
It sure took a lot of reading to follow along, but there is a much easier way to describe all the geometric properties of multi-dimensional structures. The following chart below shows all the properties of multi-dimensional structures, even beyond the seventh dimension, up to the thirteenth dimension!
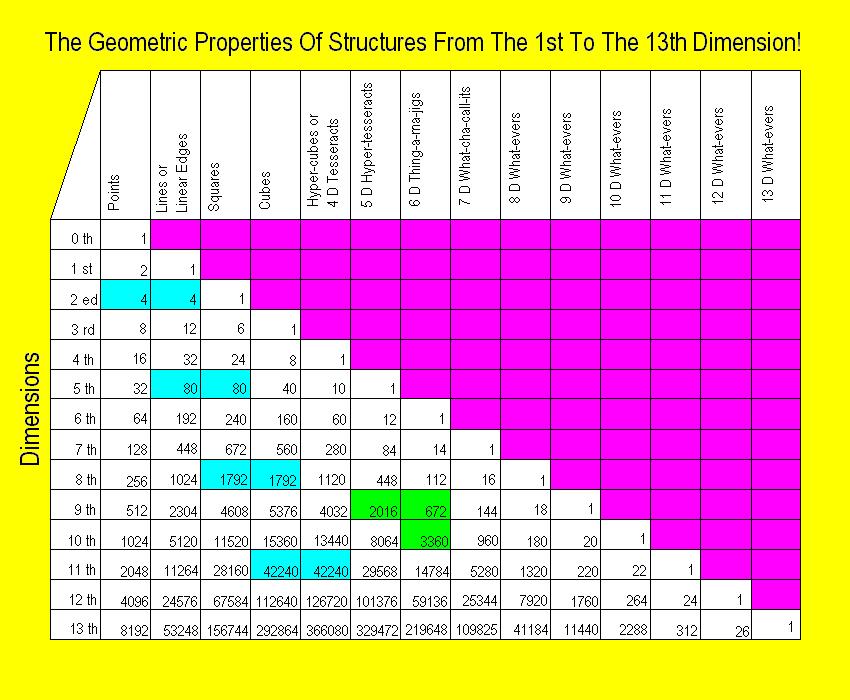
Notice the blue rectangles. They indicate number pairs that occur in the second, fifth, eight, and eleventh dimensions. The two-dimensional square has four corners, and four edges. The five-dimensional hyper-tesseract has eighty linear edges and eighty squares. The eight-dimensional what-ever has one thousand seven hundred and ninety two squares and one thousand seven hundred and ninety two cubes. And the eleven dimensional what-ever has forty two thousand two hundred and forty cubes and forty two thousand two hundred and forty hyper-cubes! The next number pair will occur at the fourteenth, seventeenth, twentieth, twenty third, etc, etc, dimensions. These number pairs occur every third dimension. Each number in the chart is the result of doubling the number directly above it, and adding it's adjacent number to the left, as indicated by the green rectangles. So, I have given you the information you need if you wish to keep on extending the chart to even higher dimensions. If in the process, you don't notice any more number pairs, it means you have made a mistake in adding. Believe me I should know! I had to go over the calculations three different times before I got it right!
Now we shall go on to rectangular structures, from the second dimension, up to the seventh dimension.
Rectangular structures are a little bit more complicated. Actually, a lot more complicated. so, I won't lie to you. OK? With squares, cubes, hypercubes, etc. etc. all the sides are equal in length, where as, with two-dimensional rectangles, you have sides of different lengths. With three-dimensional rectangular solids you have rectangular faces with different surfaces areas. With four-dimensional rectangular hyper-solids, you have rectangular solids with different volumes, etc. etc.
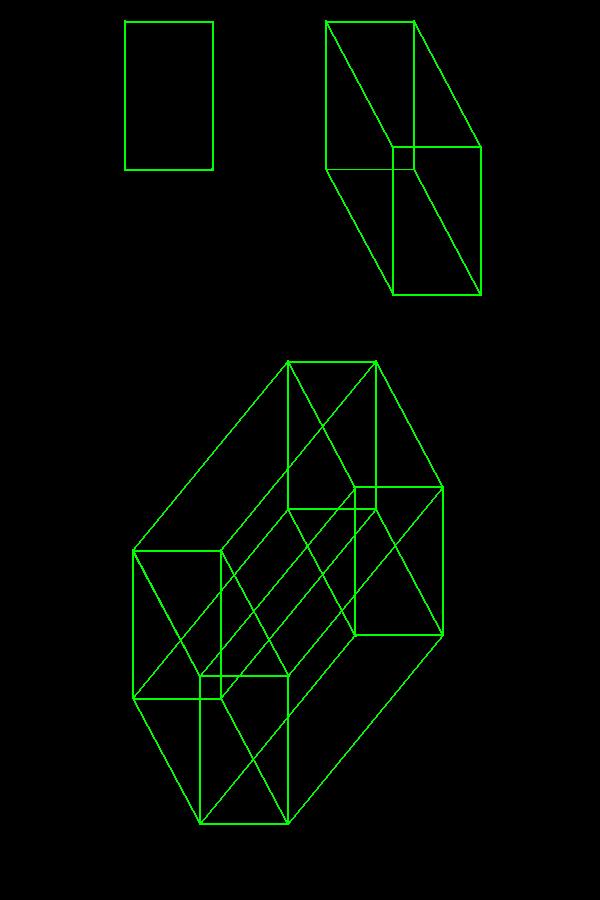 Here we see three examples of the two-dimensional rectangle, the three-dimensional rectangular solid, and a four-dimensional rectangular hyper-structure.
Here we see three examples of the two-dimensional rectangle, the three-dimensional rectangular solid, and a four-dimensional rectangular hyper-structure.
Let us say that the two-dimensional rectangle measures three units wide, and five units tall. Like the square it has four corners, and four linear edges, with two edges being three feet long, and two edges being five feet long. The total length of the four sides, or the perimeter of the rectangle is 3+3+5+5=16 feet. Since the rectangle measures three feet, by five feet, the interior area is 3x5=15 square feet.
Like the cube, the three-dimensional rectangular solid has twelve linear edges, and six surfaces. It measures three feet by five feet, by seven feet. It has four linear edges that are three feet long, four edges that are five feet long, and four edges that are seven feet in length. The total length of the twelve edges is: (4x3)+(4x5)+(4x7)=12+20+28=60 feet.
The three-dimensional rectangular solid has two surfaces measuring 3x5=15 square feet, two surfaces 3x7=21 square feet feet, and two surfaces measuring 7x5=35 square feet, for a total surface area of:
(2x15)+(2x21)+(2x35)=30+48+70=148 square feet.
Since the rectangular solid measures three by five by seven, it has an interior volume of 3x5x7=105 cubic feet.
The four-dimensional rectangular hyper-solid, like the hyper cube, has thirty two linear edges, twenty four surfaces, and eight, three-dimensional hyper-surfaces. Our rectangular hyper-solid measures three feet, by five feet, by seven feet, by eleven feet. (I'm using prime numbers) Therefore, of the thirty two linear edges, it has eight linear edges measuring three feet long, eight edges measuring five feet in length, eight edges measuring seven feet long, and eight edges that are eleven feet in length. The total length of all the thirty two linear edges is:
(8x3)+(8x5)+(8x7)+(8x11)=24+40+56+88=208 feet.
Of the twenty four surfaces, four of them are 3x5=15 square feet, four of them are 3x7=21 square feet, four of them are 3x11=33 square feet, four of them are 5x7=35 square feet, four of them are 5x11=55 square feet, and four of them are 7x11=77 square feet for a total area of:
4x(15+21+33+35+55+77)=4x236=944 square feet.
Of the eight, three-dimensional hyper surfaces, two of them are 3x5x7=105 cubic feet, two of them are 3x5x11=165 cubic feet, two of them are 5x7x11=385 cubic feet, and two of them are 3x7x11=222 cubic feet, with a total hyper-surface volume of:
2x(105+165+385+222)=2x877=1754 cubic feet.
Since our four-dimensional rectangular hyper-solid measures three by five by seven by eleven, it has a total interior hyper-volume of 3x5x7x11=1155 hyper-cubic feet.
I case you're wondering, why didn't I make the rectangular hyper-solid, 3x5x7x9 feet? Why 3x5x7x11 feet instead? Because when it comes to using odd numbers, I happen to like prime numbers. A prime number is divisible only by itself and by one. Eventually I'll tell you why I'm using prime numbers.
Now we shall move on to The Fifth Dimension. But instead of giving long drawn out verbal descriptions of multi-dimensional rectangular structures, or drawings, all the properties of these multi-dimensional rectangular structures can be charted, as seen in the following examples.
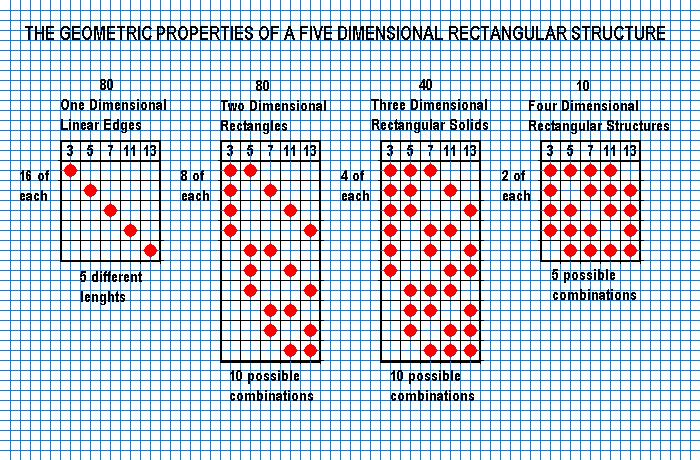
Notice that the number of possible combinations are 5, 10, 10, and 5. Keep these numbers in mind, or write them down to help you remember. Actually you don't have to write them down, we'll go back to them again. Now lets go on the The Sixth Dimension.
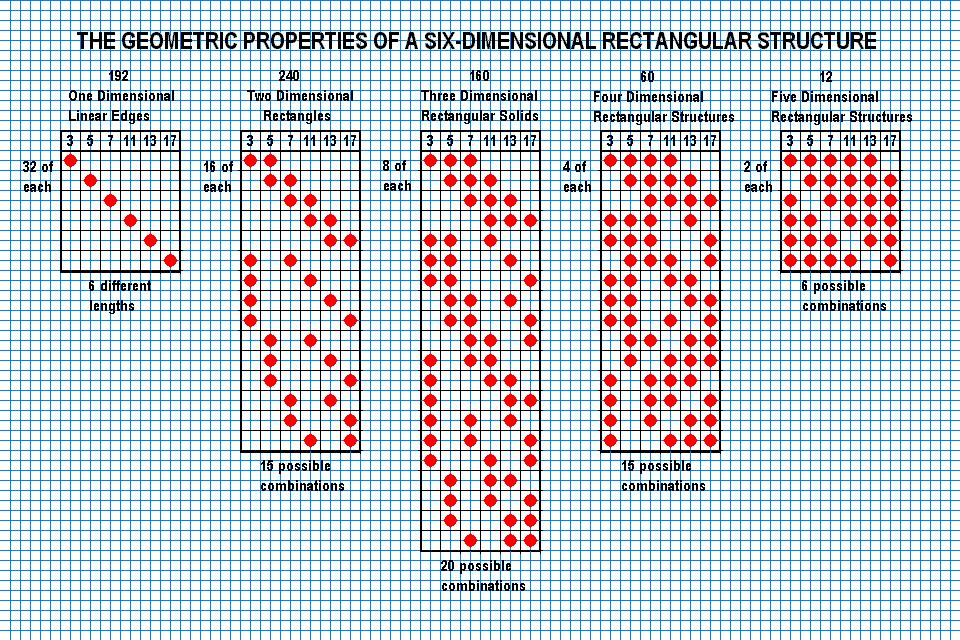
Again, notice that the number of possible combinations are 6, 15, 20, 15, and 6. Again, keep these numbers in mind, we will go back to them again, now on to The Seventh Dimension.

Finally, notice that the number of possible combinations are 7, 21, 35, 35, 21, and 7. Now then, just what is so special about these numbers? Well, they happen to be the coefficients of the binomial (a+b) raised to the 5th, 6th, and 7th powers. For example, the coefficients of the binomial raised to the power of zero, is 1. Anything raised to the power of zero is 1.
The coefficients of the binomial (a+b) raised to the first power, are 1 and 1
The coefficients of the binomial (a+b) to the second power, or squared (a+b)x(a+b) are 1 ,2 , and 1.
The coefficients of the binomial (a+b) raised to the third power, or cubed (a+b)x(a+b)x(a+b) are 1, 3, 3, and 1.
The coefficients of the binomial (a+b) raised to the fourth power are 1, 4, 6, 4, and 1
The coefficients of the binomial (a+b) raised to the fifth power are 1, 5, 10, 10, 5, and 1
The coefficients of the binomial (a+b) raised to the sixth power are 1, 6, 15, 20, 15, 6, and 1
The coefficients of the binomial (a+b) raised to the seventh power are 1, 7, 21, 35, 35, 21, 7, and 1
Now you shall see what is so special about these numbers. What a coincidence, that the numbers of possible combinations happen to correspond to the coefficients of binomials raised to various powers. These numbers can be arranged in a triangle, like The Magic Triangle below, know as Pascal's Triangle, which was discovered by the 17th century mathematician Blaise Pascal.
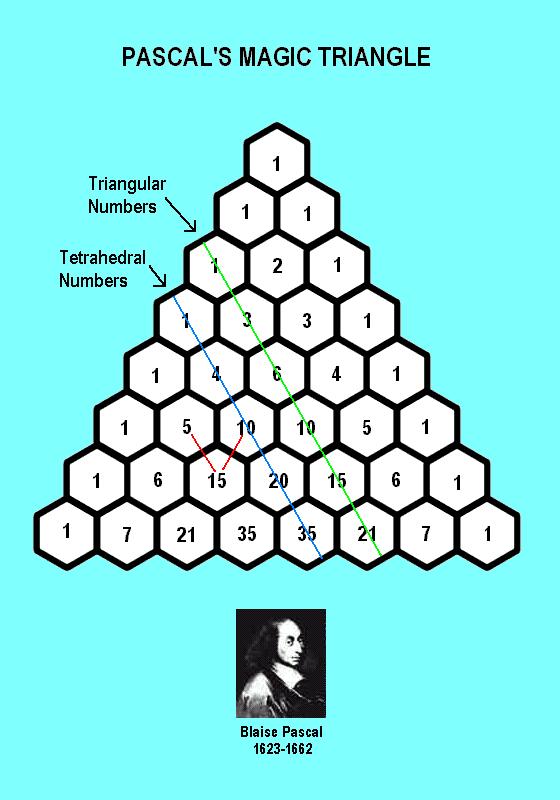
Notice that each number, is the sum of two adjacent numbers in the row above it, for example, the 15 in the seventh row, is the sum of the 5 and 10 in the sixth row above the 15, as indicated by the red lines. Also notice that the numbers along the green diagonal line, are triangular numbers, the number of objects that can be arranged in a triangle, for example, 10 bowling pins, or a rack of 15 pool balls. The numbers along the blue diagonal line are tetrahedral numbers, which is the number of spheres that can be stacked in a three-dimensional tetrahedral arrangement. The next diagonal, which is not indicated by any colored line, are what I call pentatope numbers. A pentatope is a four-dimensional triangular structure with five exterior tetrahedral hyper-surfaces. The next diagonal would be triangular structures in five dimensions. Pascals Triangle can be used to predict the coefficients of binomials raised to ever higher powers. Also the bigger the Magic Triangle becomes, the more diagonals it has, and the higher the number of dimensions they describe. Pascal's Triangle is truly a Magic Triangle, because it is the key to unlocking the mathematical door to higher dimensions. Pascal's Magic Triangle can be used as a reference, a guide to see if you have made any mistakes in your calculations, and it lets you know the number of possible combinations, for example: the 35 possible combinations of 4 out of 7 numbers, for the different sizes of four-dimensional rectangular structures that make up the seven-dimensional rectangular what-cha-call-it! (Damn! I wish some mathematician had made up names to call these things!) And so, our next subject will be, multi-dimensional triangular structures.
But first, let me tell you why I prefer to use prime numbers for my multi-demensional rectangular structures.
Let us say for example, that astronomers had received an intelligent signal from deep space, with their radio telescopes, and we wish to reply. We could start by sending a simple black and white image, using a binary code of ones and zeros. The ones could represent white pixels, and the zeros could represent black pixels. We would then send a string of ones and zeros that would repeat over and over again. Now here is where prime numbers come in. Let us say for example we send a repeating string of 302303 black and white pixels. This number can only be broken down into two prime factors of 503 and 601. This would mean that we are sending them a picture that is 601 pixels wide, and 503 pixels tall.
Now suppose, for example: we wish to send then a simple animated cartoon, that repeats over and over again, and the animation is made up of 1009 pictures. we would then send them a binary string of 305023727 black and white pixels, represented by ones and zeros. This number can only be broken down into three prime factors of 503, 601, and 1009, which would make up a three-dimensional matrix of black and white pixels. This could only be interpreted as 1009 pictures measuring 503 by 601 pixels. And so, you would have sent a simple cartoon-like animation made up of 1009 pictures. That's why prime numbers would be used, because the only way to break down the number 305023727, is by it's three prime factors of 1009, 601, and 503. There can be no other interpretation. If we were to send a repeating string of 610962525181 binary ones and zeros, this can only be broken down into four prime factors, 503, 601, 1009, and 2003, and so, it could only be interpreted as a four-dimensional matrix. You can send all kind of information, encoded in a multi-dimensional matrix. The number of ones and zeros must be a product of prime numbers. So, if you want to have your information encoded in a seven-dimensional matrix, the long repeating string of ones and zeros would have to be a product of seven prime numbers. Neat! Eh? Now you know why I love prime numbers!

